
Fractions... Fact vs Fiction
Fact: Fractions is a topic that is controversial with people when it comes to math.
Fiction: Fractions are scary!
Fact: You CAN teach fractions with meaning.
Fiction: If I have to draw a picture of the fraction, that means I'm not good at math.
Fact: Making fractions conceptual, using manipulatives, and changing how we (the teachers) talk about fractions can have a HUGE IMPACT on student understanding in our fraction standards.
When I first started teaching back in 2005, I personally, did not have a conceptual understanding of fractions. To be honest, it wasn't until about 2010 ( I was 27 years old) and I attended a professional development in Columbus, Ohio that I started to really comprehend what a fraction truly was. I was never taught that a fraction is part of a whole. I was taught rules and procedures. That's it.
When Kristin was moved from 3rd grade to 4th grade and became a teammate across the hall, we were both on a journey to understand our standards better. We wanted to know more of the WHY not just the HOW when it came to mathematics.
When I changed HOW I taught my students, not only did their learning soar, but mine did as well. One of the first things I changed was the vocabulary I was using. Most students would come to me as a 4th grader and know that the top number in a fraction was called the "numerator" and the bottom number was called the "denominator". A lot of teachers would be happy with that, but when my students couldn't tell me what "numerator" and "denominator" meant, I knew I had to rectify that. Kristin and I came together and said, "What do we need students to know when it comes to meaning of fractions?" Here's what we came up with.
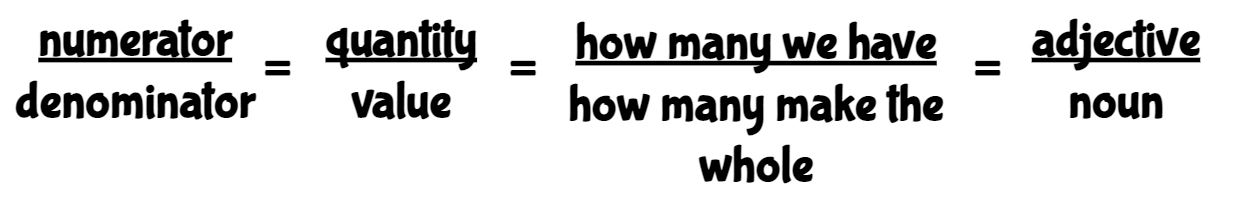 I have had so many students come into 4th grade and struggle with adding fractions with like denominators that I take it back to how our primary friends do one to one correspondence with addition.
I have had so many students come into 4th grade and struggle with adding fractions with like denominators that I take it back to how our primary friends do one to one correspondence with addition.
In kindergarten we ask our students to count like this.
1 bear + 1 bear + 1 bear = 3 bears or 2 rings + 3 rings = 5 rings
The numbers tell us our quantity, the bear and ring says what we are counting or our value.
number = quantity = adjective
object = value = noun
Let's give it a go with fractions.
1/2 + 1/2 + 1/2 = 3/2
Why? Why is it not 3/6? Let's dive in...
When we rewrite this same problem in unit form, 1 half + 1 half + 1 half, it allows the students to see that we are adding halves. Halves is the object in which we are adding. They can see that 1 half + 1 half + 1 half = 3 halves.
We are adding 1 + 1 + 1 to get 3 and we are adding halves.
Almost the exact situation happened on the 2nd day of school this year. Take a look at the picture below from when we added our second half for the school year. A student gave the answer of 1/2 + 1/2 = 2/4. I got out manipulatives and we added 1 block + 1 block to equal 2 blocks. I got out fraction tiles and built 1 half + 2 half. The class was able to see that we didn't have fourths. It wasn't 4 parts that equaled 1 whole, but 2 halves. We built our way to writing it out below.
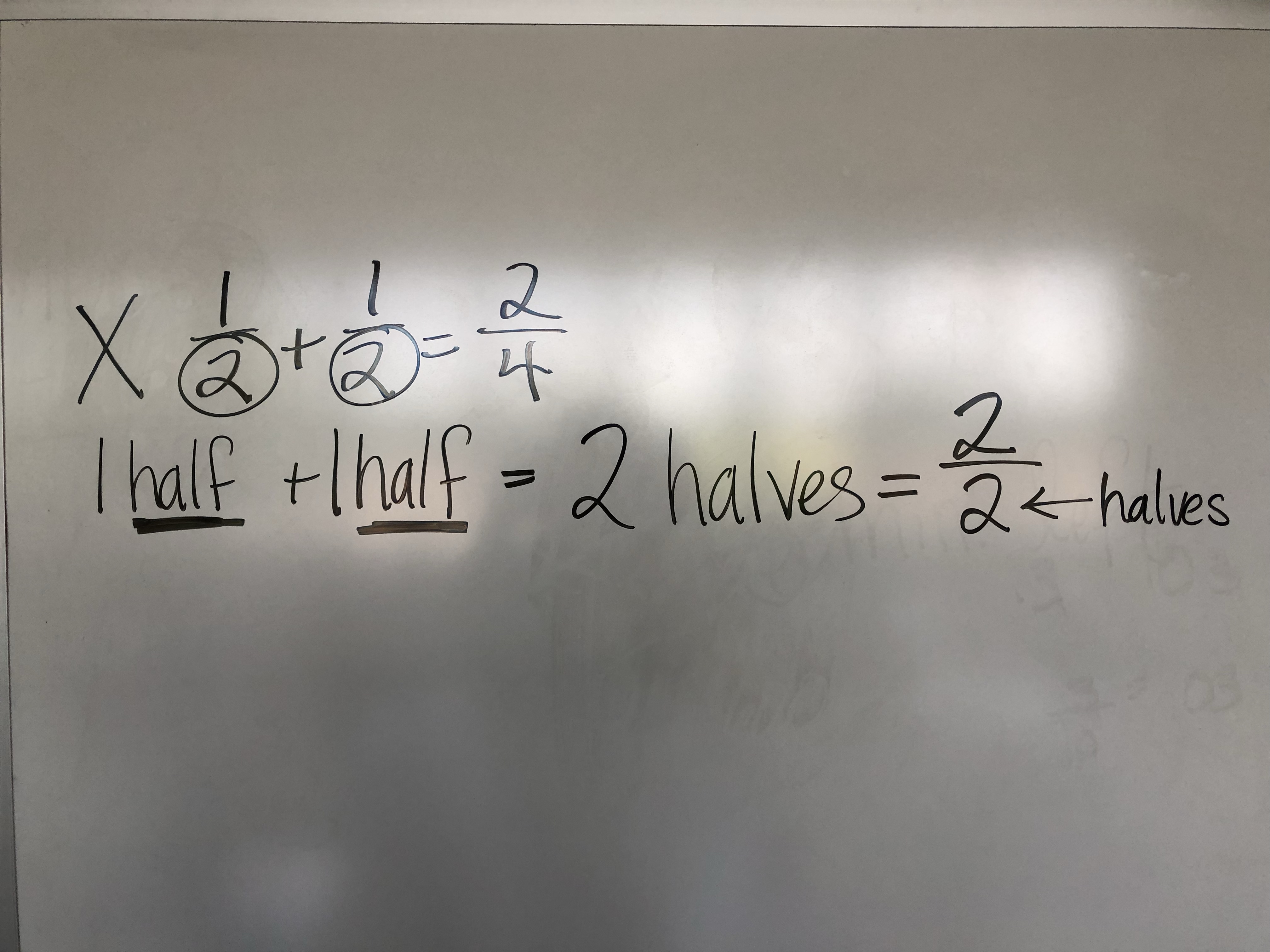
The same thing can be used if we are adding bigger values and different units ...
3/4 + 3/4= ?
3 fourths + 3 fourths = 6 fourths = 6/4
Some of you might be wondering... What about when we add fractions with unlike denominators? That my friends is for another blog post. :)

Feel free to download the Fraction Vocab below to use in your classroom to help with fractions in your classroom.